Matrix calculation is considered as one of the most challenging data manipulation task. First time when i was asked to compute sum of diagonal cells in a range, i thought it would be a easy job. Later i realized it's a brain scratching riddle and spent a good amount of time to crack it. In this tutorial, we would cover how to sum cells down a diagonal or up a diagonal.
Suppose you have data in range B3:G8 (as shown in the image below). You want to sum the diagonal cells of a range.
Let's break the first formula and explain each step
ROW($B$3:$G$8)
The ROW Function returns the row number of a reference.
In this case, it returns the values 3,4,5,6,7,8. This represents the row number of the table you are summing up (if the table started at say B2, then the first number would be a 2).
MAX(ROW(B3:G8)
It returns the column number. In this case, it returns 2,3,4,5,6,7 (starting at 2 because the first column is B)
MAX(COLUMN($B$3:$G$8))
Excel takes TRUE as 1 and FALSE as 0. We are telling Excel to multiple TRUE/FALSE matrix with the original values in B3:G8.
=SUMPRODUCT((ROW($B$3:$G$8)-MAX(ROW(B3:G8))=COLUMN($B$3:$G$8)-MAX(COLUMN(B3:G8)))*($B$3:$G$8))
The SUMPRODUCT function returns the SUM of the products of a range. In this case, it is not taking products of two ranges. Instead, it is summing up the matrix shown in the image below.
The only difference between the two formulas is MIN/MAX of rows and columns. In this case, we are taking MIN as we need to sum of cells up a diagonal. See the detailed explanation in the comments below.
Download the workbook
Suppose you have data in range B3:G8 (as shown in the image below). You want to sum the diagonal cells of a range.
Paste the following formula in cell I3 and copy it down a column
=SUMPRODUCT((ROW($B$3:$G$8)-MAX(ROW(B3:G8))=COLUMN($B$3:$G$8)-MAX(COLUMN(B3:G8)))*($B$3:$G$8))II. Sum cells up a diagonal
=SUMPRODUCT((ROW($B$3:$G$8)-MIN(ROW(B3:G8))=MIN(COLUMN(B3:G8))-COLUMN($B$3:$G$8))*($B$3:$G$8))
Let's break the first formula and explain each step
ROW($B$3:$G$8)
The ROW Function returns the row number of a reference.
In this case, it returns the values 3,4,5,6,7,8. This represents the row number of the table you are summing up (if the table started at say B2, then the first number would be a 2).
MAX(ROW(B3:G8)
It returns 8 as 8th row is the maximum row in the range B3:G8. It is the row number of cell G8.
ROW($B$3:$G$8)-MAX(ROW(B3:G8)
Then we are subtracting 8 from (3,4,5,6,7,8)
= (3,4,5,6,7,8) - 8 which is equal to (-5, -4, -3, -2, -1, 0)COLUMN($B$3:$G$8)
It returns the column number. In this case, it returns 2,3,4,5,6,7 (starting at 2 because the first column is B)
MAX(COLUMN($B$3:$G$8))
It returns 7 as column number of G8 is 7
COLUMN($B$3:$G$8)-MAX(COLUMN(B3:G8)
It subtracts 7 from (2,3,4,5,6,7) which is equivalent to (-5,-4,-3,-2,-1,0)
(ROW($B$3:$G$8)-MAX(ROW(B3:G8))=COLUMN($B$3:$G$8)-MAX(COLUMN(B3:G8)))
It compares the above two matrix and returns TRUE where value of both the matrix is equal to 0.
 |
| Logical Condition |
(ROW($B$3:$G$8)-MAX(ROW(B3:G8))=COLUMN($B$3:$G$8)-MAX(COLUMN(B3:G8)))*($B$3:$G$8)
Excel takes TRUE as 1 and FALSE as 0. We are telling Excel to multiple TRUE/FALSE matrix with the original values in B3:G8.
 |
| Diagonal Cells |
The SUMPRODUCT function returns the SUM of the products of a range. In this case, it is not taking products of two ranges. Instead, it is summing up the matrix shown in the image below.
1 + 6 + 9 +13 + 1 + 5 = 35
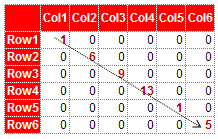 |
| Sum of cells down a diagonal |
The only difference between the two formulas is MIN/MAX of rows and columns. In this case, we are taking MIN as we need to sum of cells up a diagonal. See the detailed explanation in the comments below.
Download the workbook




Hi, it is a great site, I would like to suggest that you please explain your formulas as how it works and the logic behind, so it will be more useful than just copying as it is without understanding it. Thanks!
ReplyDeleteThank you for your feedback. I have added the description. Cheers!
DeleteDUDE!!!! AWESOME. saved me about 2 weeks of copying and pasting data diagonally.
ReplyDeleteThank you for your appreciation!
DeleteI agree with comment on 10 Dec 2014. That would also help with tweaking the formula to suit own situation (size of triangle and what it is that you are trying to sum).
ReplyDeleteI have added the explanation. Thanks!
DeleteGreat formula, thanks a lot. Since you saved ne a lot of processing power with sharing this formula, I will now take the time to explain how it works to your subscribers whom queries it. This is a nice and elegant solution, well done.
ReplyDeleteI am breaking the formula down and explain what each step in it does:
>> ROW($B$3:$G$8)
returns the values 3,4,5,6,7,8. This represents the row number of the table you are summing up (if the table started at say B2, then the first number would be a 2). If you enter that part of the formula into an array (select 5 rows, type in the formula and then press CTRL + SHIFT + ENTER) then you will see that result
>> -MIN(ROW(B3:G8))
returns the smallest row number from the array above, being a 3 in this scenario. Again, if you want to see the output just enter the formula into an array.
>>(ROW($B$3:$G$8)-MIN(ROW(B3:G8))
if we combine the above two parts of the equation, then we basically get a "matrix" that reads, 0,1,2,3,4,5 which is effectively the row number of the cell you are trying to sum.
(3 - 3 = 0, 4 - 3 = 1, 5 - 3 = 2 etc)
>>=MIN(COLUMN(B3:G8))
This returns 2 for all the values (because the table starts at column B). You can test it by selecting 6 columns (one row) enter the formula and then press (CTRL+SHIFT+ENTER)
>>-COLUMN($B$3:$G$8))
Basically returns the column number, being 2,3,4,5,6,7 (starting at 2 because the first column is B). You can validate it by selecting 6 columns (one row) and pressing CTRL+SHIFT+ENTER
>> MIN(COLUMN(B3:G8))-COLUMN($B$3:$G$8))
combining the above two basically indicate a counter for the column you are working in, being 0,-1,-2,-3,-4,-5
>>(ROW($B$3:$G$8)-MIN(ROW(B3:G8))=MIN(COLUMN(B3:G8))-COLUMN($B$3:$G$8))
the above function now compares the two matrixes with each other, the "row" part looking like this:
0 0 0 0 0 0
1 1 1 1 1 1
2 2 2 2 2 2
3 3 3 3 3 3
4 4 4 4 4 4
5 5 5 5 5 5
while the Column part looks like this:
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
The only two cells that have a matching value is the top left cell, as per the below boolean table:
TRUE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
>> *($B$3:$G$8)
this means that it will only sumproduct the parts of the matrix that is TRUE, being the top left cell.
hence the result for the first cell.
If you look carefully at the formula, you will notice that the min parts of the columns and rows is not fixed, as such, as you move the formula down one row, the matrices looks like this:
ROWS: -1 -1 -1 -1 -1 -1
0 0 0 0 0 0
1 1 1 1 1 1
2 2 2 2 2 2
3 3 3 3 3 3
4 4 4 4 4 4
COLS
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
0 -1 -2 -3 -4 -5
since we only copied it one row down and did not shift the columns the result looks the same
and the boolean matrix looks like this:
FALSE TRUE FALSE FALSE FALSE FALSE
TRUE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
FALSE FALSE FALSE FALSE FALSE FALSE
and so forth.
as mentioned, great formula, well written.
Regards
Skouperd
(www.skoups.com)
Awesome! Thank you for taking the time to explain the formula in detail. I have added the explanation to the article.
DeleteMy pleasure. Glad you could use it.
DeleteRegards
Skouperd
Hi, Is there any way to use this dynamically within a table? I have a table which expands weekly and need to sum the diagonals. I am manually updating some very long equations but it would be far simpler and more practical to have it expand automatically as the table does. Any direction in this would be really appreciated
ReplyDeleteJust wanted to say THANK YOU! This formula was exactly what I was looking for, and it's an elegant solution that does require array formulas (which most people who are using the spreadsheet I created don't understand).
ReplyDeleteHow do i sum everything above and below 1,6,9,13,1,5?
ReplyDelete