Partial correlation measures linear relationship between two variables, while controlling the effect of one or more variable. In this tutorial, we will see the difference between partial and semipartial correlation and how these statistical metrics are calculated mathematically. Also we will cover how it is used in regression analysis.
What is Partial Correlation?
Partial correlation explains the correlation between two continuous variables (let's say X1 and X2) holding X3 constant for both X1 and X2.
Partial Correlation Mathematical Formula
In this case, r12.3 is the correlation between variables x1 and x2 keeping x3 constant. r₁3 is the correlation between variables x1 and x3.
Let's take an example -
Suppose we want to see the relationship between sales and number of high performing employees keeping promotion budget constant. In this case, sales is the variable1 and high performing employees is the variable 2 and promotion budget the variable3.
Examples
What is Semipartial Correlation
Semipartial correlation measures the strength of linear relationship between variables X1 and X2 holding X3 constant for just X1 or just X2. It is also called part correlation.
In the above image, r1(2.3) means the semipartial correlation between variables X1 and X2 where X3 is constant for X2.
Difference between Partial and Semipartial Correlation
SAS Code : Partial Correlation Coefficient
In this example, we are checking association between height and weight keeping age constant.
The partial correlation coefficient between weight and height is 0.70467 holding age constant. The p-value for the coefficient is 0.0011. It means we can reject the null hypothesis and concludes that coefficient is significantly different from zero.
R Script : Partial Correlation Coefficient
R Script : Semipartial Correlation Coefficient
Semi partial correlation - Age constant for Weight only
estimate p.value statistic n gp Method
0.4118409 0.08947395 1.807795 19 1 pearson
The estimate value is Pearson Semipartial correlation coefficient.
Semi partial correlation coefficient - Age constant for Height only
1 0.4732797 0.04727912 2.149044 19 1 pearson
Squared Partial and Semipartial Correlation
In regression, squared partial and squared semipartial correlation coefficients are used.
Squared partial correlation tells us how much of the variance in dependent variable (Y) that is not explained by variable X2 but explained by X1. In other words, it is the proportion of the variation in dependent variable that was left unexplained by other predictors / independent variables but has been explained by independent variable X1.
Here, R²y.12 is the r-squared from the regression model in which X1 and X2 are independent variables.
Squared Semi-partial correlation tells us how much of the unique contribution of an independent variable to the total variation in dependent variable. In other words, it explains increment in R-square when an independent variable is added.
Squared Partial correlation will always be greater than or equal to squared semi-partial correlation.
In PROC REG, the PCORR2 option tells SAS to produce squared-partial correlation and SCORR2 option tells SAS to produce squared semi-partial correlation. The STB option is used to generate standardized estimate and TOL is used to calculate tolerance.
Partial correlation explains the correlation between two continuous variables (let's say X1 and X2) holding X3 constant for both X1 and X2.
Partial Correlation Mathematical Formula
In this case, r12.3 is the correlation between variables x1 and x2 keeping x3 constant. r₁3 is the correlation between variables x1 and x3.
 |
| Partial Correlation |
Let's take an example -
Suppose we want to see the relationship between sales and number of high performing employees keeping promotion budget constant. In this case, sales is the variable1 and high performing employees is the variable 2 and promotion budget the variable3.
 |
| Formula : Compute Partial Correlation |
- Relationship between demand of coffee and tea keeping prices of tea controlled.
- Relationship between GMAT score and number of hours studied keeping SAT score constant.
- Relationship between weight and number of meals intake while controlling age
- Relationship between bank deposits and interest rate keeping household rate constant.
What is Semipartial Correlation
Semipartial correlation measures the strength of linear relationship between variables X1 and X2 holding X3 constant for just X1 or just X2. It is also called part correlation.
 |
| Semipartial Correlation |
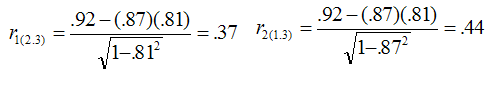 |
| Semi Partial Correlation Score |
Difference between Partial and Semipartial Correlation
Partial correlation holds variable X3 constant for both the other two variables. Whereas, Semipartial correlation holds variable X3 for only one variable (either X1 or X2). Hence, it is called 'semi'partial.Assumptions : Partial and Semipartial Correlation
- Variables should be continuous in nature. For example, weight, GMAT score, sales etc
- There should be linear relationship between all the three variables. If a variable has non-linear relationship, transform it or ignore the variable.
- There should be no extreme values (i.e outliers). If outliers are present, we need to treat them either by percentile capping or remove the outlier observations
- Variables you want to hold constant can be one or more than one
SAS Code : Partial Correlation Coefficient
In this example, we are checking association between height and weight keeping age constant.
PROC CORR data=sashelp.class;
Var Height;
With weight;
Partial age;
Run;
 |
| Partial Correlation Coefficient |
The partial correlation coefficient between weight and height is 0.70467 holding age constant. The p-value for the coefficient is 0.0011. It means we can reject the null hypothesis and concludes that coefficient is significantly different from zero.
R Script : Partial Correlation Coefficient
# Load Library
library(ppcor)
# Read data
mydata=read.csv("C:\\Users\\Deepanshu\\Documents\\Example1.csv")
# Partial correlation between "height" and "weight" given "age"
with(mydata, pcor.test(Height,Weight,Age))
Semi partial correlation - Age constant for Weight only
with(mydata, spcor.test(Height,Weight,Age))Output
estimate p.value statistic n gp Method
0.4118409 0.08947395 1.807795 19 1 pearson
The estimate value is Pearson Semipartial correlation coefficient.
Semi partial correlation coefficient - Age constant for Height only
with(mydata, spcor.test(Weight,Height,Age))estimate p.value statistic n gp Method
1 0.4732797 0.04727912 2.149044 19 1 pearson
Squared Partial and Semipartial Correlation
In regression, squared partial and squared semipartial correlation coefficients are used.
Squared partial correlation tells us how much of the variance in dependent variable (Y) that is not explained by variable X2 but explained by X1. In other words, it is the proportion of the variation in dependent variable that was left unexplained by other predictors / independent variables but has been explained by independent variable X1.
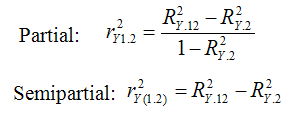 |
| Squared Partial and Semipartial Correlation |
Here, R²y.12 is the r-squared from the regression model in which X1 and X2 are independent variables.
Squared Semi-partial correlation tells us how much of the unique contribution of an independent variable to the total variation in dependent variable. In other words, it explains increment in R-square when an independent variable is added.
Squared Partial correlation will always be greater than or equal to squared semi-partial correlation.
Squared Partial Correlation >= Squared Semi-partial Correlation
SAS Code : Squared Partial and Semi-Partial Correlation
In PROC REG, the PCORR2 option tells SAS to produce squared-partial correlation and SCORR2 option tells SAS to produce squared semi-partial correlation. The STB option is used to generate standardized estimate and TOL is used to calculate tolerance.
Proc Reg data= Readin;
Model Overall = VAR1 - VAR5 / SCORR2 PCORR2 STB TOL ;
run;
 |
| Regression Output |
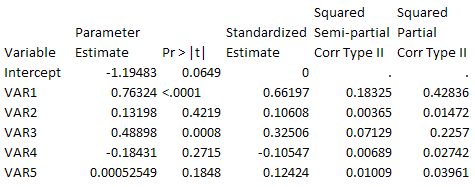
The squared semi-partial correlation between Overall and VAR1 tells us model R-square is added by 0.18325 if VAR1 is included in the model.
The squared partial correlation between Overall and VAR1 tells us the proportion of variance in Overall that is not explained by the other independent variables, 43% is explained by VAR1.
Which indicates variable importance?
Answer is NO. It is because the total variation in dependent variable also constitutes a portion that is due to within correlation between two independent variables.
Which indicates variable importance?
Squared Semipartial correlation indicates variable importance because it measures incremental value in R-Square. We can rank variables based on high to low values of squared semipartial correlation score.
Relationship between Squared Semipartial correlation and Standardized Estimate
Relationship between Squared Semipartial correlation and Standardized Estimate
Squared Semipartial Correlation = (Standardized Estimate)² * Tolerance
Can individual squared semi-partial correlation add to R-squared?
Answer is NO. It is because the total variation in dependent variable also constitutes a portion that is due to within correlation between two independent variables.


what is difference between correlation and partial correlation ?
ReplyDeletewhen you are talking about just 2 variables then correlation comes but if you are talking about more than 2 variables then partial correlation comes into picture. So,basically partial correlation is also between 2 variables but controlling the effect of other variables
ReplyDeleteoverall about the site and very useful stuff you maintained here. Keep up the good work and stay blessed always. Fareed
ReplyDeleteWhat is the dfference between squared partial corr type 1 and squared partial corr type 2? and likewise what's the difference between squared semipartial corr type 1 and squared semipartial corr type 2. What ddoes Type 1 and Type 2 represent? When do you use Type 1 and when do you use Type 2?
ReplyDelete