Logistic Regression
It is used to predict the result of a categorical dependent variable based on one or more continuous or categorical independent variables. In other words, it is multiple regression analysis but with a dependent variable is categorical.
Examples
1. An employee may get promoted or not based on age, years of experience, last performance rating etc. We are trying to calculate the factors that affects promotion. In this case, two possible categories in dependent variable : "Promoted" and "Not Promoted".
2. We are interested in knowing how variables, such as age, sex, body mass index, effect blood pressure (sbp). In this case, two possible categories in dependent variable : "High Blood Pressure" and "Normal Blood Pressure".
Algorithm
Logistic regression is based on Maximum Likelihood (ML) Estimation which says coefficients should be chosen in such a way that it maximizes the Probability of Y given X (likelihood). With ML, the computer uses different "iterations" in which it tries different solutions until it gets the maximum likelihood estimates. Fisher Scoring is the most popular iterative method of estimating the regression parameters.
Take exponential both the sides
Distribution
Example - If you flip a coin twice, what is the probability of getting one or more heads? It's a binomial distribution with N=2 and p=0.5. The binomial distribution consists of the probabilities of each of the possible numbers of successes on N trials for independent events that each have a probability of p.
Interpretation of Logistic Regression Estimates
If X increases by one unit, the log-odds of Y increases by k unit, given the other variables in the model are held constant.
In logistic regression, the odds ratio is easier to interpret. That is also called Point estimate. It is exponential value of estimate.
For Continuous Predictor
Magnitude : If you want to compare the magnitudes of positive and negative effects, simply take the inverse of the negative effects. For example, if Exp(B) = 2 on a positive effect variable, this has the same magnitude as variable with Exp(B) = 0.5 = ½ but in the opposite direction.
These are Chi-Square tests. They test against the null hypothesis that at least one of the predictors' regression coefficient is not equal to zero in the model.
Important Performance Metrics
It looks at maximum difference between distribution of cumulative events and cumulative non-events.
Interpret Results :
1. Odd Ratio of GRE (Exp value of GRE Estimate) = 1.002 implies for a one unit increase in gre, the odds of being admitted to graduate school increase by a factor of 1.002.
It is used to predict the result of a categorical dependent variable based on one or more continuous or categorical independent variables. In other words, it is multiple regression analysis but with a dependent variable is categorical.
Examples
1. An employee may get promoted or not based on age, years of experience, last performance rating etc. We are trying to calculate the factors that affects promotion. In this case, two possible categories in dependent variable : "Promoted" and "Not Promoted".
2. We are interested in knowing how variables, such as age, sex, body mass index, effect blood pressure (sbp). In this case, two possible categories in dependent variable : "High Blood Pressure" and "Normal Blood Pressure".
Algorithm
Logistic regression is based on Maximum Likelihood (ML) Estimation which says coefficients should be chosen in such a way that it maximizes the Probability of Y given X (likelihood). With ML, the computer uses different "iterations" in which it tries different solutions until it gets the maximum likelihood estimates. Fisher Scoring is the most popular iterative method of estimating the regression parameters.
logit(p) = b0 + b1X1 + b2X2 + ------ + bk Xkwhere logit(p) = loge(p / (1-p))
Take exponential both the sides
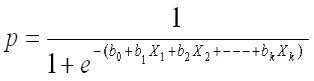 |
| Logistic Regression Equation |
p : the probability of the dependent variable equaling a "success" or "event".
 |
| Logistic Regression Curve |
Distribution
Binary logistic regression model assumes binomial distribution of the response with N (number of trials) and p(probability of success). Logistic regression is in the 'binomial family' of GLMs. The dependent variable does not need to be normally distributed.
Example - If you flip a coin twice, what is the probability of getting one or more heads? It's a binomial distribution with N=2 and p=0.5. The binomial distribution consists of the probabilities of each of the possible numbers of successes on N trials for independent events that each have a probability of p.
Interpretation of Logistic Regression Estimates
If X increases by one unit, the log-odds of Y increases by k unit, given the other variables in the model are held constant.
For Continuous Predictor
An unit increase in years of experience increases the odds of getting a job by a multiplicative factor of 4.27, given the other variables in the model are held constant. In other words, the odds of getting a job are increased by 327% (4.27-1)*100 for an unit increase in years of experience.For Binary Predictor
The odds of a person having years of experience getting a job are 4.27 times greater than the odds of a person having no experience.Note : To calculate 5 unit increase, 4.27 ^ 5 (instead of multiplication).
Magnitude : If you want to compare the magnitudes of positive and negative effects, simply take the inverse of the negative effects. For example, if Exp(B) = 2 on a positive effect variable, this has the same magnitude as variable with Exp(B) = 0.5 = ½ but in the opposite direction.
Odd Ratio (exp of estimate) less than 1 ==> Negative relationship (It means negative coefficient value of estimate coefficients)
Standardized Coefficients
The concept of standardization or standardized coefficients (aka estimates) comes into picture when predictors (aka independent variables) are expressed in different units. Suppose you have 3 independent variables - age, height and weight. The variable 'age' is expressed in years, height in cm, weight in kg. If we need to rank these predictors based on the unstandardized coefficient, it would not be a fair comparison as the unit of these variable is not same.
Standardized Coefficients (or Estimates) are mainly used to rank predictors (or independent or explanatory variables) as it eliminate the units of measurement of independent and dependent variables). We can rank independent variables with absolute value of standardized coefficients. The most important variable will have maximum absolute value of standardized coefficient.Interpretation of Standardized Coefficient
A standardized coefficient value of 2.5 explains one standard deviation increase in independent variable on average, a 2.5 standard deviation increase in the log odds of dependent variable.
 |
| Standardized Coefficient : Logistic Regression |
Assumptions of Logistic Regression
- The logit transformation of the outcome variable has a linear relationship with the predictor variables. The one way to check the assumption is to categorize the independent variables. Transform the numeric variables to 10/20 groups and then check whether they have linear or monotonic relationship.
- No multicollinearity problem. No high correlationship between predictors.
- No influential observations (Outliers).
- Large Sample Size - It requires at least 10 events per independent variable.
Test Overall Fit of the Model : -2 Log L , Score and Wald Chi-Square
These are Chi-Square tests. They test against the null hypothesis that at least one of the predictors' regression coefficient is not equal to zero in the model.
Important Performance Metrics
1. Percent Concordant : Percentage of pairs where the observation with the desired outcome (event) has a higher predicted probability than the observation without the outcome (non-event).
Rule: Higher the percentage of concordant pairs the better is the fit of the model. Above 80% considered good model.
2. Percent Discordant : Percentage of pairs where the observation with the desired outcome (event) has a lower predicted probability than the observation without the outcome (non-event).
3. Percent Tied : Percentage of pairs where the observation with the desired outcome (event) has same predicted probability than the observation without the outcome (non-event).
4. Area under curve (c statistics) - It ranges from 0.5 to 1, where 0.5 corresponds to the model randomly predicting the response, and a 1 corresponds to the model perfectly discriminating the response.
C = Area under Curve = %concordant + (0.5 * %tied)
.90-1 = excellent (A)
.80-.90 = good (B)
.70-.80 = fair (C)
.60-.70 = poor (D)
.50-.60 = fail (F)
5. Classification Table (Confusion Matrix)
Sensitivity (True Positive Rate) - % of events of dependent variable successfully predicted as events.
Sensitivity = TRUE POS / (TRUE POS + FALSE NEG)
Specificity (True Negative Rate) - % of non-events of dependent variable successfully predicted as non-events.
Specificity = TRUE NEG / (TRUE NEG + FALSE POS)
Correct (Accuracy) = Number of correct prediction (TRUE POS + TRUE NEG) divided by sample size.
6. KS Statistics
Detailed Explanation - How to Check Model Performance
Problem Statement -
A researcher is interested in how variables, such as GRE (Graduate Record Exam scores), GPA (grade point average) and prestige of the undergraduate institution, affect admission into graduate school. The outcome variable, admit/don't admit, is binary.
This data set has a binary response (outcome, dependent) variable called admit, which is equal to 1 if the individual was admitted to graduate school, and 0 otherwise. There are three predictor variables: gre, gpa, and rank. We will treat the variables gre and gpa as continuous. The variable rank takes on the values 1 through 4. Institutions with a rank of 1 have the highest prestige, while those with a rank of 4 have the lowest. [Source : UCLA]
Download Data
This data set has a binary response (outcome, dependent) variable called admit, which is equal to 1 if the individual was admitted to graduate school, and 0 otherwise. There are three predictor variables: gre, gpa, and rank. We will treat the variables gre and gpa as continuous. The variable rank takes on the values 1 through 4. Institutions with a rank of 1 have the highest prestige, while those with a rank of 4 have the lowest. [Source : UCLA]
Download Data
R Code : Logistic Regression
#Read Data Filemydata <- read.csv("http://www.ats.ucla.edu/stat/data/binary.csv")#Summarysummary(mydata)#Cross Tabxtabs(~admit + rank, data = mydata)#Data Preparationmydata$rank <- factor(mydata$rank)# Split data into training (70%) and validation (30%)dt = sort(sample(nrow(mydata), nrow(mydata)*.7))train<-mydata[dt,]val<-mydata[-dt,]# Check number of rows in training and validation data setsnrow(train)nrow(val)#Run Logistic Regressionmylogistic <- glm(admit ~ ., data = train, family = "binomial")summary(mylogistic)$coefficient#Stepwise Logistic Regressionmylogit = step(mylogistic)#Logistic Regression Coefficientsummary.coeff0 = summary(mylogit)$coefficient#Calculating Odd RatiosOddRatio = exp(coef(mylogit))summary.coeff = cbind(Variable = row.names(summary.coeff0), OddRatio, summary.coeff0)row.names(summary.coeff) = NULL#R Function : Standardized Coefficientsstdz.coff <- function (regmodel){ b <- summary(regmodel)$coef[-1,1]sx <- sapply(regmodel$model[-1], sd)beta <-(3^(1/2))/pi * sx * breturn(beta)}std.Coeff = data.frame(Standardized.Coeff = stdz.coff(mylogit))std.Coeff = cbind(Variable = row.names(std.Coeff), std.Coeff)row.names(std.Coeff) = NULL#Final Summary Reportfinal = merge(summary.coeff, std.Coeff, by = "Variable", all.x = TRUE)#Predictionpred = predict(mylogit,val, type = "response")finaldata = cbind(val, pred)#Storing Model Performance Scoreslibrary(ROCR)pred_val <-prediction(pred ,finaldata$admit)# Maximum Accuracy and prob. cutoff against itacc.perf <- performance(pred_val, "acc")ind = which.max( slot(acc.perf, "y.values")[[1]])acc = slot(acc.perf, "y.values")[[1]][ind]cutoff = slot(acc.perf, "x.values")[[1]][ind]# Print Resultsprint(c(accuracy= acc, cutoff = cutoff))# Calculating Area under Curveperf_val <- performance(pred_val,"auc")perf_val# Plotting Lift curveplot(performance(pred_val, measure="lift", x.measure="rpp"), colorize=TRUE)# Plot the ROC curveperf_val2 <- performance(pred_val, "tpr", "fpr")plot(perf_val2, col = "green", lwd = 1.5)#Calculating KS statisticsks1.tree <- max(attr(perf_val2, "y.values")[[1]] - (attr(perf_val2, "x.values")[[1]]))ks1.tree
Interpret Results :
1. Odd Ratio of GRE (Exp value of GRE Estimate) = 1.002 implies for a one unit increase in gre, the odds of being admitted to graduate school increase by a factor of 1.002.
2. AUC value shows model is not able to distinguish events and non-events well.
3. The model can be improved further either adding more variables or transforming existing predictors.


This is very very useful for new comers. I strongly recommend this.
ReplyDeleteThanks sir ...best efforts....
ReplyDeleteThank you for your appreciation!
DeleteHi Folk,
ReplyDeleteThanks for providing this wonderful article.
When I ran the below code it showed me an error.
#Prediction
pred = predict(logit,type="response")
Error in predict.lm(object, newdata, se.fit, scale = 1, type = ifelse(type == :
object 'val' not found
You have not copied the code correctly. Check the code once again. You forgot to mention validation data set name in the predict function.
DeleteHi Deepanshu,
ReplyDeleteROC is the graph between sensitivity and 1- specificity
Then how could you plot it in between True and False positive
It is the same thing. Sensitivity is True Positive Rate. (1-Specificity) is False Positive Rate.
Deletegreat explanation of what can be a tricky concept to grasp at first
ReplyDeletenice
ReplyDeleteI would appreciate if you can demonstrate sas codes for logistic regression. many thanks for for your help so far
ReplyDeletei'm getting an error
ReplyDeleteError in fix.by(by.x, x) : 'by' must specify a uniquely valid column
on executing
final = merge(summary.coeff,std.Coeff,by = "Variable", all.x = TRUE)
please help!
Hi Deepanshu, Can You please explain what is the functionality of Predict and predition function logit regression and what is process of calculating performance of model
ReplyDeleteHi, While doing Dimension Reduction...Would you consider it doing it on the data before training/Validation split?
ReplyDeleteHello Sir,
ReplyDeleteThank you for this amazing post.
I am facing with problem while running a particular code :
print(c(accuracy= acc, cutoff= cutoff))
Error in print(c(accuracy = acc, cutoff = cutoff)) :
object 'acc' not found
can you please advise regarding this , the performance function "acc.perf" executed perfectly.
Hello. Thank you for this great work.
ReplyDeleteI am receiving aN ERROR:
> xtabs(~admit + rank, data = mydata)
Error in eval(expr, envir, enclos) : object 'admit' not found
Any input is welcome!
data has been moved to:
ReplyDeletemydata <- read.csv("http://www.ats.ucla.edu/stat/data/binary.csv")
oops copy/pasted the old address. The new address is:
Deletemydata <- read.csv("https://stats.idre.ucla.edu/stat/data/binary.csv")
I am getting an error:
ReplyDelete> std.Coeff = data.frame(Standardized.Coeff = stdz.coff(mylogit))
Error in var(if (is.vector(x) || is.factor(x)) x else as.double(x), na.rm = na.rm) :
Calling var(x) on a factor x is defunct.
Use something like 'all(duplicated(x)[-1L])' to test for a constant vector.
I am getting an error for these line of codes...
ReplyDeletestd.Coeff<-data.frame(Standardized.Coeff = stdz.coff(mylogit))
std.Coeff<-cbind(Variable = row.names(std.Coeff), std.Coeff)
row.names(std.Coeff) = NULL
the error message is:
std.Coeff<-data.frame(Standardized.Coeff = stdz.coff(mylogit))
Error in var(if (is.vector(x) || is.factor(x)) x else as.double(x), na.rm = na.rm) :
Calling var(x) on a factor x is defunct.
Use something like 'all(duplicated(x)[-1L])' to test for a constant vector. > std.Coeff<-cbind(Variable = row.names(std.Coeff), std.Coeff)
Error in row.names(std.Coeff) : object 'std.Coeff' not found
> row.names(std.Coeff) = NULL
Error in row.names(std.Coeff) = NULL : object 'std.Coeff' not found
In the line "sx <- sapply(regmodel$model[-1], sd)" change [-1] to [1]. I did this and followed along.
DeleteHello!
ReplyDeletei am getting an error:
> std.Coeff = data.frame(Standardized.Coeff = stdz.coff(mylogit))
Error in var(if (is.vector(x) || is.factor(x)) x else as.double(x), na.rm = na.rm) :
Calling var(x) on a factor x is defunct.
Use something like 'all(duplicated(x)[-1L])' to test for a constant vector.
can u help what it's mean?
In the line "sx <- sapply(regmodel$model[-1], sd)" change [-1] to [1] and the problem "Error in var(if (is.vector(x) || is.factor(x)) x else as.double(x), na.rm = na.rm) : Calling var(x) on a factor x is defunct.
ReplyDeleteUse something like 'all(duplicated(x)[-1L])' to test for a constant vector." was gone.