How to calculate partial correlation matrix in Excel

This article explains how to compute partial correlation matrix in MS Excel.

Partial Correlation

It is simply defined as the measure of the relationship between two or more variables while controlling for the effects of one or more additional variables.

For example, study of partial correlation between price and demand would involve studying the relationship between price and demand excluding the effect of price of related goods, disposable income, taste and preference etc.

Derivation using Matrix Inversion

1. Compute correlation matrix

=CORREL(OFFSET(firstvariable_range ,,ROWS($1:1)-1),OFFSET(firstvariable_range,,COLUMNS($A:A)-1))

For example, you have a 4 X 4 matrix and data for variables are entered in cells A2:D8 so paste this formula in cell G3 =

CORREL(OFFSET($A$2:$A$8,,ROWS($1:1)-1),OFFSET($A$2:$A$8,,COLUMNS($A:A)-1))

In this case, firstvariable_range is A2:A8.

For detailed explanation, visit this link Correlation Matrix using Excel Formula

Download the workbook used in this example so you can copy and paste the formula

2. Compute inverse matrix

MINVERSE is the function which returns the inverse matrix stored in an array.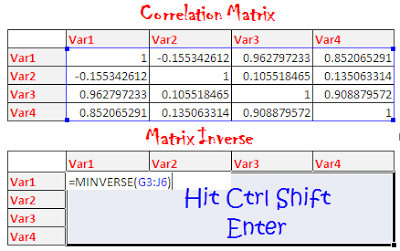

How to use :
Select N rows and N columns.
For example, correlation matrix is stored in G3:J6. Select cells from G9 to J12

Apply MINVERSE formula. =MINVERSE(G3:J6) and Hit Ctrl Shift Enter to confirm it.

After confirming this with Ctrl Shift Enter, you will find {=MINVERSE(G3:J6)} across all the cells in matrix.

3. Compute Partial correlation matrix

Partial correlation in cell(x,y) = inverse in cell(x,y) / (-1* Square root(inverse in cell(x,x) * inverse in cell(y,y))

To make it dynamic so that it works if number of variables changes i used the formula below.

=G9/(-1*SQRT(ABS(OFFSET($G$9,ROW(A1)-1,ROW(A1)-1)*OFFSET($G$9,COLUMN(A1)-1,COLUMN(A1)-1))))

Here, G9 is a cell reference of inverse in (var1,var1). This reference changes when you paste the formula across all the cells in matrix.

Download this workbook
Related link : Partial Correlation UDF

Related Posts

Excel Tutorials : Top 100 Excel Tutorials

Spread the Word!
Share Share Tweet

About Author:

Deepanshu founded ListenData with a simple objective - Make analytics easy to understand and follow. He has over 10 years of experience in data science. During his tenure, he worked with global clients in various domains like Banking, Insurance, Private Equity, Telecom and HR.

While I love having friends who agree, I only learn from those who don't
Let's Get Connected Email LinkedIn