There are two main measures for assessing performance of a predictive model :
- Discrimination
- Calibration
These measures are not restricted to logistic regression. They can be used for any classification techniques such as decision tree, random forest, gradient boosting, support vector machine (SVM) etc. The explanation of these two measures are shown below -
1. Discrimination
Discrimination refers to the ability of the model to distinguish between events and non-events.
It plots true positive rate (aka Sensitivity) and false positive rate (aka 1-Specificity). Mathematically, It is calculated using the formula below -
AUC = Concordant Percent + 0.5 * Tied Percent

Concordant : Percentage of pairs where the observation with the desired outcome (event) has a higher predicted probability than the observation without the outcome (non-event).
Discordant : Percentage of pairs where the observation with the desired outcome (event) has a lower predicted probability than the observation without the outcome (non-event).
Tied : Percentage of pairs where the observation with the desired outcome (event) has same predicted probability than the observation without the outcome (non-event).
- If AUC>= 0.9, the model is considered to have outstanding discrimination. Caution : The model may be faced with problem of over-fitting.
- If 0.8 <= AUC < 0.9, the model is considered to have excellent discrimination.
- If 0.7<= AUC < 0.8, the model is considered to have acceptable discrimination.
- If AUC = 0.5, the model has no discrimination (random case)
- If AUC < 0.5, the model is worse than random
It is a common measure for assessing predictive power of a credit risk model. It measures the degree to which the model has better discrimination power than the model with random scores.
Somer's D = 2 AUC - 1 or Somer's D = (Concordant Percent - Discordant Percent) / 100
It should be greater than 0.4.
It looks at maximum difference between distribution of cumulative events and cumulative non-events.
- KS statistics should be in top 3 deciles.
- KS statistics should be between 40 and 70.
 |
| KS Statistics |
In this case, KS is maximum at second decile and KS score is 75.
Calculating KS Test with SASIt implies the model should predict the highest number of events in the first decile and then goes progressively down. For example, there should not be a case that the decile 2 predicts higher number of events than the first decile.
2. Calibration
It is a measure of how close the predicted probabilities are to the actual rate of events.
It measures the association between actual events and predicted probability.
In HL test, null hypothesis states that sample of observed events and non-events supports the claim about the predicted events and non-events. In other words, the model fits data well.
Calculation- Calculate estimated probability of events
- Split data into 10 sections based on descending order of probability
- Calculate number of actual events and non-events in each section
- Calculate Predicted Probability = 1 by averaging probability in each section
- Calculate Predicted Probability = 0 by subtracting Predicted Probability=1 from 1
- Calculate expected frequency by multiplying number of cases by Predicted Probability = 1
- Calculate chi-square statistics taking frequency of observed (actual) and predicted events and non-events
 |
| Hosmer Lemeshow Test |
Rule : If p-value > .05. the model fits data well
The null hypothesis states the model fits the data well. In other words, null hypothesis is that the fitted model is correct.
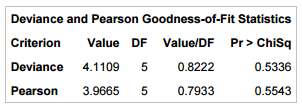 |
| Deviance and Residual Test |
Since p-value is greater than 0.05 for both the tests, we can say the model fits the data well.
In SAS, these tests can be computed by using option scale = none aggregate in PROC LOGISTIC.
The Brier score is an important measure of calibration i.e. the mean squared difference between the predicted probability and the actual outcome.
Lower the Brier score is for a set of predictions, the better the predictions are calibrated.
- If the predicted probability is 1 and it happens, then the Brier Score is 0, the best score achievable.
- If the predicted probability is 1 and it does not happen, then the Brier Score is 1, the worst score achievable.
- If the predicted probability is 0.8 and it happens, then the Brier Score is (0.8-1)^2 =0.04.
- If the predicted probability is 0.2 and it happens, then the Brier Score is (0.2-1)^2 =0.64.
- If the predicted probability is 0.5, then the Brier Score is (0.5-1)^2 =0.25, irregardless of whether it happens.
By specifying fitstat option in proc logistic, SAS returns Brier score and other fit statistics such as AUC, AIC, BIC etc.
proc logistic data=train; model y(event="1") = entry; score data=valid out=valpred fitstat; run;
A complete assessment of model performance should take into consideration both discrimination and calibration. It is believed that discrimination is more important than calibration.
SAS Macro : Best Model Selection

Awesome work man :)....great site keep it up...please add arima also :)
ReplyDeleteThank you for your appreciation. Check out the series of ARIMA articles -
Deletehttp://www.listendata.com/search/label/Time%20Series
In the above tabulate of Hosmers lemeshow u were supposed to create 10 deciles but I can see only 8.
ReplyDeleteI have also noticed 8 deciles instead of 10 deciles
DeleteThank you for putting this site together. You're explanations are so clear and straight to the point; very helpful.
ReplyDeleteCannot open the macro file..is it password protected?
ReplyDeleteCannot open the macro file..is it password protected?
ReplyDeleteHi, thanks for the post. The file "SAS Macro : Best Model Selection" requires a password. Whats the password ?
ReplyDeleteWhats the password for the excel macro? if you are not providing the password then why you upload and make visible?
ReplyDeleteWhats the Password for Macro file
ReplyDeletepassword for macro file?
ReplyDeleteHi, kindly provide us with the macro passwords fro the excel file
ReplyDelete