In predictive modeling, dimensionality reduction or dimension reduction is the process of reducing the number of irrelevant variables. It is a very important step of predictive modeling. Some predictive modelers call it 'Feature Selection' or 'Variable Selection'. If the idea is to improve accuracy of the model, it's the step wherein you need to invest most of your time. Right variables produce more accurate models. Hence, it is required to build some variable reduction /selection strategies to build the robust predictive model. Some of these strategies are listed below -
Step I : Remove Redundant Variables
The following 3 simple analysis helps to remove redundant variables
- Remove variables having high percentage of missing values (say 50%)
- Remove Zero and Near Zero-Variance Predictors
- Remove highly correlated variables (greater than 0.7). The absolute values of pair-wise correlations are considered. If two variables have a high correlation, look at the mean absolute correlation of each variable and removes the variable with the largest mean absolute correlation. See how it works -
The sample correlation matrix is shown below -
Corrmatrix <- structure(c(1, 0.82, 0.54, 0.36, 0.85, 0.82, 1, 0.01, 0.74, 0.36,
0.54, 0.01, 1, 0.65, 0.91, 0.36, 0.74, 0.65, 1, 0.36,
0.85, 0.36, 0.91, 0.36, 1),
.Dim = c(5L, 5L))
Steps :
- First, take absolute values of correlation matrix (Use abs(Corrmatrix) function in R)
- Replace all diagonal values (1s) in the matrix with NAs (Use diag(Corrmatrix) <- NA)
- Compute mean of each column.
- Calculate rank of the mean values (calculated in Step 3) on descending order.
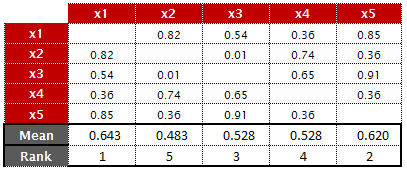 |
| Average of Columns |
5. Reorder correlation matrix based on the Rank.
 |
| Updated Correlation Matrix |
6. Now, checks if the matrix(i,j) > cutoff, then calculates the following steps -
- Mean value of the row of matrix( i , ). For example, for the variables(x1,x5), the mean value of first row is 0.642
- Mean of the row of matrix( -j , ). For variables (x1,x5), the mean value of all rows (except second row) is 0.545
Since x1 has the highest mean absolute correlation value, removes variable 'x1'.
In the next iteration, it checks for the variables (x5,x3) excluding x1. It would be a comparison of mean of (0.91 0.36 0.36) vs. mean of (0.91 0.36 0.36 0.36 0.65 0.74 0.36 0.01 0.74)
How to do it in R
The findCorrelation() function from caret package performs the above steps.
The findCorrelation() function from caret package performs the above steps.
library(caret)
findCorrelation(Corrmatrix, cutoff = .6, verbose = TRUE, names = TRUE)
It returns the variables that are highly correlated and can be removed prior to building a model.
Step II : Feature Selection with Random Forest
Random Forest is one of the most popular machine learning algorithm in data science. The best part of this algorithm is there are no assumptions attached to it as regression techniques have. The pre-processing work is very less as compared to other techniques. It overcomes the problem of overfitting that decision tree has. One of the output it produces - It provides a list of predictor (independent) variables which are important in predicting the target (dependent) variable. It contains two measures of variable importance. The first one - Gini gain produced by the variable, averaged over all trees.
Download : Example Dataset
R Code : Removing Redundant Variables
R Code : Feature Selection with Random Forest
Random Forest is one of the most popular machine learning algorithm in data science. The best part of this algorithm is there are no assumptions attached to it as regression techniques have. The pre-processing work is very less as compared to other techniques. It overcomes the problem of overfitting that decision tree has. One of the output it produces - It provides a list of predictor (independent) variables which are important in predicting the target (dependent) variable. It contains two measures of variable importance. The first one - Gini gain produced by the variable, averaged over all trees.
The second one - Permutation Importance i.e. mean decrease in classification accuracy after permuting the variable, averaged over all trees. Sort the permutation importance score on descending order and select the TOP k variables.
Since the permutation variable importance is affected by collinearity, it is necessary to handle collinearity prior to running random forest for extracting important variables.
Download : Example Dataset
R Code : Removing Redundant Variables
# load required libraries
library(caret)
library(corrplot)
library(plyr)
# load required dataset
dat <- read.csv("C:\\Users\\Deepanshu Bhalla\\Downloads\\pml-training.csv")
# Set seed
set.seed(227)
# Remove variables having high missing percentage (50%)
dat1 <- dat[, colMeans(is.na(dat)) <= .5]
dim(dat1)
# Remove Zero and Near Zero-Variance Predictors
nzv <- nearZeroVar(dat1)
dat2 <- dat1[, -nzv]
dim(dat2)
# Identifying numeric variables
numericData <- dat2[sapply(dat2, is.numeric)]
# Calculate correlation matrix
descrCor <- cor(numericData)
# Print correlation matrix and look at max correlation
print(descrCor)
summary(descrCor[upper.tri(descrCor)])
# Check Correlation Plot
corrplot(descrCor, order = "FPC", method = "color", type = "lower", tl.cex = 0.7, tl.col = rgb(0, 0, 0))
# find attributes that are highly corrected
highlyCorrelated <- findCorrelation(descrCor, cutoff=0.7)
# print indexes of highly correlated attributes
print(highlyCorrelated)
# Indentifying Variable Names of Highly Correlated Variables
highlyCorCol <- colnames(numericData)[highlyCorrelated]
# Print highly correlated attributes
highlyCorCol
# Remove highly correlated variables and create a new dataset
dat3 <- dat2[, -which(colnames(dat2) %in% highlyCorCol)]
dim(dat3)
R Code : Feature Selection with Random Forest
library(randomForest)
#Train Random Forest
rf <-randomForest(classe~.,data=dat3, importance=TRUE,ntree=1000)
#Evaluate variable importance
imp = importance(rf, type=1)
imp <- data.frame(predictors=rownames(imp),imp)
# Order the predictor levels by importance
imp.sort <- arrange(imp,desc(MeanDecreaseAccuracy))
imp.sort$predictors <- factor(imp.sort$predictors,levels=imp.sort$predictors)
# Select the top 20 predictors
imp.20<- imp.sort[1:20,]
print(imp.20)
# Plot Important Variables
varImpPlot(rf, type=1)
# Subset data with 20 independent and 1 dependent variables
dat4 = cbind(classe = dat3$classe, dat3[,c(imp.20$predictors)])



great article. I am learning R and this was very helpful indeed. Please keep writing more hands on how to do this in R stuff:-)
ReplyDeletecheers
Manish
Glad you liked it. Stay tuned :-)
DeleteHi Manish, nice article.
ReplyDeleteOne question
If we are removing highly correlated variables, do we keep one variable among the highly correlated set (cluster) to represent the other removed variables of the set or do we remove all of them?
No, it keeps one variable among the 2 highly correlated variables. If two variables have a high correlation, the function looks at the mean absolute correlation of each variable and removes the SINGLE variable with the largest mean absolute correlation.
DeleteWhat do you mean by mean absolute correlation of each variable? How can we compute the correlation of a single variable? Thanks.
DeleteI have added more description in the article. Hope it helps.
DeleteHi Deepanshu,
ReplyDeleteThanks for your very useful code. I am getting error in the mtry command as mentioned below. Any clue to solve that ?
mtry <- tuneRF(dat3[, -36], dat3[,36], ntreeTry=1000, stepFactor=1.5,improve=0.01, trace=TRUE, plot=TRUE)
mtry = 5 OOB error = 0%
Searching left ...
mtry = 4 OOB error = 0%
NaN 0.01
Error in if (Improve > improve) { : missing value where TRUE/FALSE needed
It is because OOB error is very small. Scope of improvement is very minimal. Hence, improve = 0.01 fails. You can ignore this line of code and just to the next step. Set 4 to mtry instead of mtry = best.m. See the code below -
Deleterf <-randomForest(classe~.,data=dat3, mtry=4, importance=TRUE,ntree=1000)
Really like the way you have created a whole correlation module. Thanks. Any other articles you have written on pre-analytics visualization in R?
ReplyDeleteWhat a informative post! It's really helpful.
ReplyDeleteBut I have a question. findCorrelation() function searches columns to remove to reduce pair-wise correlations. Then, is it different with vif() function?
vif() function calculates multi-collinearity. what's the difference?
with this i know i'm not alone in data science
ReplyDelete