In this article, we will cover how to compute Variance Inflation Factor (VIF) in SAS.
What is Variance Inflation Factor?
The Variance Inflation Factor (VIF) is used to assess multicollinearity in a multiple regression model. Multicollinearity occurs when two or more independent variables in a regression model are highly correlated with each other.
Multicollinearity leads to problems in interpreting the coefficients of individual independent variables in a regression model. To detect multicollinearity, VIF measures how much the variance of the estimated coefficients increases when the variables are correlated compared to when they are not correlated.
The steps to calculate VIF for each independent variable in a regression model are as follows:
- For each independent variable (predictor), a separate regression model is run, considering that predictor as the dependent variable and all other predictors as independent variables.
- For each independent variable, calculate its VIF using the following formula:
VIF = 1 / (1-R^2)where R-squared value obtained from the regression model in the previous step.
The rule of thumb for VIF is as follows:
- VIF between 1 and 5: Moderate multicollinearity (not a major concern).
- VIF above 5: High multicollinearity (may lead to unreliable coefficient estimates).
How to Calculate Variance Inflation Factor (VIF) in SAS
The option VIF in MODEL statement in PROC REG tells SAS to calculate and display the Variance Inflation Factor (VIF) for each of the independent variables. The following SAS code produces regression results along with the VIF values for each of the independent variables. It helps you to assess potential multicollinearity issues in the model.
PROC REG DATA=sashelp.cars; MODEL MPG_City = EngineSize Weight Length Horsepower / VIF ; RUN;
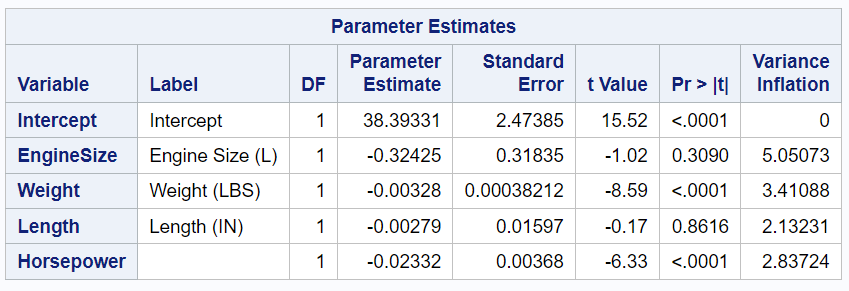
Here we are using the dependent variable "MPG_City" and four independent variables: "EngineSize", "Weight", "Length" and "Horsepower".
VIF for the variable EngineSize is 5.05073. Since it is greater than 5, it indicates a multicollinearity issue. This means that the coefficient estimates and p-values in the regression model are not reliable for use.
How to Save VIF Values in a SAS Dataset
The following code creates a dataset containing the VIF for each independent variable using the ODS OUTPUT statement.
ods output ParameterEstimates=vif; PROC REG DATA=sashelp.cars; MODEL MPG_City = EngineSize Weight Length Horsepower / VIF ; RUN; proc print data=vif noobs; var varianceinflation; where VarianceInflation> 5 and variable ^= "Intercept"; run;
How to Solve Multicollinearity Problem in SAS
To solve the multicollinearity problem, we can perform "stepwise variable selection" based on Variance Inflation Factor (VIF) values. See the calculation steps below-
- Calculate the VIF for each independent variable in the model.
- Identify the independent variable with the highest VIF greater than 5.
- Remove the variable identified in step 2 from the model.
- Recalculate the VIF values for the remaining independent variables after the removal.
- Repeat steps 2 to 4 until the highest VIF among the remaining variables falls below the predetermined threshold (e.g., 5).
- Stop the iterative process once all remaining independent variables have VIF values below the threshold.
SAS Macro: Stepwise Variable Selection based on VIF
The following SAS macro automates the process of calculating Variance Inflation Factor (VIF) for the independent variables in a regression model and iteratively removes variables with high VIF until all remaining variables have VIF values below a specified threshold (in this case, 5). Please note that this macro considers all the numeric variables in the dataset, excluding the dependent variable and any character or date variables, as independent variables.
The parameters of this macro are as follows:
MYDATA: Specify the name of the dataset that contains the variables for which you want to calculate the VIF and select predictors.DEPENDENTVAR: Specify the name of the dependent variable for which you want to perform the regression analysis.VIF_THRESHOLD: Sets the threshold for the maximum allowable VIF value for the predictors. The macro will continue to remove predictors iteratively until the highest VIF value is below this threshold.
%MACRO VIF_AUTO(MYDATA=,DEPENDENTVAR=,VIF_THRESHOLD=);
%LET DEPENDENTVAR = %UPCASE(&DEPENDENTVAR);
PROC CONTENTS DATA=&MYDATA. NOPRINT VARNUM OUT=FORMATOUT;
RUN;
/* Do not include dependent, character and date variables*/
/*Storing independent variables in a macro variable*/
PROC SQL NOPRINT;
SELECT NAME INTO : PREDICTORS SEPARATED BY ' '
FROM FORMATOUT
WHERE TYPE=1 AND UPCASE(NAME) NOT IN("&DEPENDENTVAR.") and FORMAT not in("DATE");
QUIT;
%LET VIF_MAX = %SYSEVALF(&VIF_THRESHOLD + 1);
%DO %UNTIL (%SYSEVALF(&VIF_MAX.<=&VIF_THRESHOLD.) );
%PUT PREDICTORS = &PREDICTORS.;
ODS OUTPUT ParameterEstimates=VIF;
PROC REG DATA=&MYDATA.;
MODEL &DEPENDENTVAR.= &PREDICTORS. / VIF ;
RUN;
QUIT;
PROC SORT DATA=VIF OUT=VIF2 ;
BY DESCENDING VarianceInflation;
WHERE VarianceInflation NOT IN(.) ;
RUN;
PROC SQL NOPRINT;
SELECT VARIABLE INTO: VAR_MAXVIF
FROM VIF2
WHERE monotonic()=1;
SELECT Variable INTO: PREDICTORS SEPARATED BY ' '
FROM VIF2
WHERE VARIABLE NOT IN("&VAR_MAXVIF.","Intercept") ;
SELECT MAX(VarianceInflation) INTO: VIF_MAX
FROM VIF2;
QUIT;
%PUT VIF_MAX=&VIF_MAX. variable_MAXVIF=&VAR_MAXVIF. ;
%END;
%global final_vars;
PROC SQL;
SELECT VARIABLE INTO : final_vars SEPARATED BY ' '
FROM VIF2
WHERE VARIABLE NOT IN("Intercept");
QUIT;
%PUT final_variables= &final_vars.;
%MEND VIF_AUTO;
%VIF_AUTO(MYDATA=sashelp.cars,DEPENDENTVAR=MPG_City,VIF_THRESHOLD=5);
This macro prints the names of the variables that passed the VIF threshold and can be used in the regression model. These final variables are stored in the macro variable named final_vars. You can also see these variables along with their VIF scores in the dataset named "VIF". To use these final variables in the regression model, you can use the macro variable "final_vars".
PROC REG DATA=sashelp.cars; MODEL MPG_City = &final_vars. / VIF ; RUN;
Another way to handle multicollinearity is by using Ridge Regression. Ridge Regression, also known as L2 regularization, is a technique that adds a penalty term to the regression equation, which is proportional to the square of the magnitude of the coefficients. This penalty term helps to shrink the coefficient estimates towards zero, reducing their variance and weakening the impact of multicollinearity.
Principal Components Regression (PCR) is another approach that can be used to address multicollinearity in regression analysis. PCR combines the concepts of Principal Component Analysis (PCA) and linear regression. PCA is a dimensionality reduction technique that transforms the original set of correlated variables (predictors) into a new set of uncorrelated variables called principal components. These principal components are linear combinations of the original predictors. PCR helps in handling multicollinearity because the principal components, being uncorrelated to each other, avoid the issue of high correlation between predictors present in the original data.
Deepanshu founded ListenData with a simple objective - Make analytics easy to understand and follow. He has over 10 years of experience in data science. During his tenure, he worked with global clients in various domains like Banking, Insurance, Private Equity, Telecom and HR.
Share Share Tweet