Linear regression helps us understand the relationship between two or more variables. It is called "linear" because it assumes that the relationship between the variables are linear.
Linear regression explains how one variable (called the "dependent variable") changes in response to changes in another variable or set of variables (called the "independent variables").
The simple linear regression model is a linear equation of the following form:
y = a + bx
- y: Dependent variable. It's the outcome we want to predict.
- a: Intercept. It is the value of y when x = 0.
- b: Slope or Coefficient. For each unit increase in x, y changes by the amount represented by the slope.
- x: Independent variable. It's the variable that explains the changes in the dependent variable y. We use it to make predictions or analyze the relationship with y.
Suppose you want to see the relationship between the amount of time a person spends studying and their exam scores. By using linear regression, you can understand how much impact study time has on exam scores.
Exam Score = a + b(Study Hours)
Here Slope (b) is the coefficient that shows how much the exam score is expected to increase (or decrease) for every one-unit increase in study hours.
The multiple linear regression model is a linear equation of the following form:
y = b0 + b1x1 + b2x2 + ... + bnxn
- y: Dependent variable. It's the outcome we want to predict.
- b0: Intercept. It is the value of y when all independent variables are 0.
- b1, b2, ..., bn: Coefficients (Slopes). Each b represents the change in y for a one-unit increase in the corresponding independent variable x1, x2, ..., xn.
- x1, x2, ..., xn: Independent variables. They are the variables that explain the changes in the dependent variable y. We use them to make predictions or analyze the relationship with y.
Suppose you want to understand the factors that influence housing prices. You have collected data on various variables such as square footage, number of bedrooms, and distance from the city center. By using multiple linear regression, you can predict how these variables collectively impact the housing prices.
Housing Price = b0 + b1(Square Footage) + b2(Number of Bedrooms) + b3(Distance from City Center)
Here each coefficient b1, b2, and b3 shows how much the housing price is expected to increase (or decrease) for a one-unit increase in square footage, number of bedrooms, and distance from the city center, respectively.
Let's create a sample dataset for the examples in this article. The following code creates a dataset containing 3 variables and 30 observations. These variables SqFoot, Distance, Price represent Square Footage, Distance from City Center and Housing Price.
data HousingPrices; input SqFoot Distance Price; datalines; 1500 10 300000 2000 15 350000 1800 12 320000 2200 18 380000 2400 20 400000 1700 8 290000 1750 9 295000 2100 17 370000 1900 11 330000 2300 16 390000 1950 11 335000 2050 14 355000 2250 17 375000 1850 10 315000 2150 15 360000 1850 9 310000 1650 7 280000 1950 11 335000 2150 18 380000 2350 21 410000 2050 14 350000 1750 6 285000 2000 10 325000 2200 19 395000 1850 12 330000 2250 20 405000 1900 11 325000 2400 18 395000 1950 13 335000 1850 8 305000 ; run;
How to Calculate Linear Regression in SAS
In SAS, there are multiple ways to build a linear regression model, and the procedures for linear regression are as follows:
- PROC REG
- PROC GLM
- PROC GLMSELECT
PROC REG : Linear Regression
The following code uses the PROC REG procedure to build a linear regression model. The variable "Price" is the dependent variable, and "SqFoot" and "Distance" are the independent (predictor) variables in the linear regression model.
ods output ParameterEstimates = estimates; proc reg data=HousingPrices; model Price = SqFoot Distance; run;
The ods output statement with the ParameterEstimates table is used to create a SAS dataset that saves the output of parameter estimates. Here we have created a dataset called "estimates".
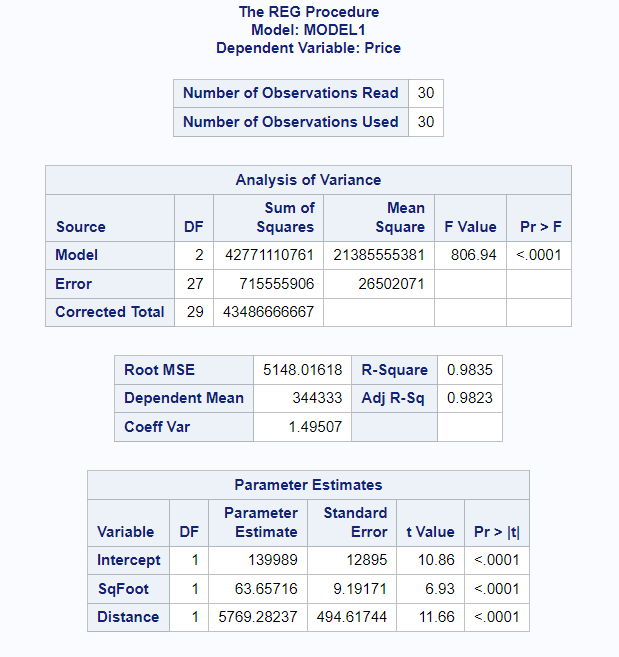
The p-value of the whole model is <.0001. Since this p-value is less than 0.05, it means the whole regression model is statistically significant.
The R-Square tells us the proportion of variation in the housing prices that can be explained by the square footage and the distance from city center. Adjusted R-squared is a more robust metric than R-squared as it considers the number of predictors and prevents overfitting in the regression model.
Higher the adjusted R-squared value, the better the independent variables are able to predict the value of the dependent variable. In this example, 0.9823 or 98.23% of the variation in the housing prices that can be explained by the square footage and the distance from city center.
The regression equation can be formed based on the parameter estimates
Housing Price = 139989 + 63.65716*(square footage) + 5769.28237*(distance from city center)
The p-value for both the independent variables is less than 0.05, which means they are statistically significant.
PROC GLM : Linear Regression
The PROC GLM has many similarities with the PROC REG procedure in terms of building a regression model. However, PROC REG is specialized for linear regression analysis with one or more continuous independent variables. Whereas the PROC GLM can handle both the categorical and continuous independent variables.
ods output ParameterEstimates = estimates; proc glm data=HousingPrices; model Price = SqFoot Distance; run;
To understand the output of the linear regression model, refer this section.
PROC GLMSELECT : Linear Regression
The benefits of using PROC GLMSELECT over PROC REG and PROC GLM for building a linear regression model are as follows:
- Handling categorical and continuous variables: PROC GLMSELECT supports categorical variables selection with CLASS statement. Whereas, PROC REG does not support CLASS statement.
- Automated variable selection: PROC GLMSELECT supports BACKWARD, FORWARD, STEPWISE variable selection techniques. Whereas, PROC GLM does not support these techniques.
ods output ParameterEstimates = estimates; PROC GLMSELECT data=HousingPrices; model Price = SqFoot Distance; run;
The CLASS statement is used to handle categorical independent variable.
PROC GLMSELECT data=dataset-name; class categorical_variable / param=ref order=data; model dependent_variable = variable1 categorical_variable / selection=stepwise select=SL showpvalues stats=all STB; run;
- selection=stepwise: This indicates that the stepwise variable selection method will be used to determine the significant predictors in the model.
- select=SL: This sets the significance level (SL) for entry and removal of variables during the stepwise selection process.
- showpvalues: This option displays the p-values for the selected variables in the output.
- stats=all: This specifies that all relevant statistics, such as parameter estimates, standard errors, and confidence intervals, will be displayed.
- STB: This option requests the standardized regression coefficients to be displayed in the output.
score data = validation out= pred_val; This line generates predicted values for the model using the "validation" dataset and stores the predicted values in a dataset named "pred_val."
PROC GLMSELECT data=dataset-name; class categorical_variable / param=ref order=data; model dependent_variable = variable1 categorical_variable / selection=stepwise select=SL showpvalues stats=all STB; score data = validation out= pred_val; run;Scoring Linear Regression Model with SAS
The CHOOSE= option allows to choose from the list of models at the steps of the selection process based on the best value of the specified criterion (Adjusted RSquare).
PROC GLMSELECT data=dataset-name; class categorical_variable / param=ref order=data; model dependent_variable = variable1 categorical_variable / CHOOSE=ADJRSQ showpvalues stats=all STB; run;
How to Check and Fix Assumptions of Linear Regression
The assumptions of linear regression are as follows:
The residuals should follow a normal distribution.
Check: Create a histogram or Q-Q plot of the residuals; they should look like a bell-shaped curve.
Fix: If the residuals are not normally distributed, consider transforming the dependent variable.
PROC GLMSELECT data=dataset-name; class categorical_variable / param=ref order=data; model dependent_variable = variable1 categorical_variable / CHOOSE=ADJRSQ showpvalues stats=all STB; output out=stdres p= predict r = resid; run; proc univariate data=stdres normal; var resid; run;
The NORMAL option in PROC UNIVARIATE generates a normality plot (Q-Q plot) to assess whether the residuals follow a normal distribution.
Homoscedasticity means the variability of residuals should be constant across all levels of the predictors.
Check: Plot the residuals against the predicted values; residuals should be evenly spread around zero, with no cone-like shape.
Fix: If heteroscedasticity is present, consider transforming the dependent variable or using weighted least squares.
PROC GLMSELECT data=dataset-name; class categorical_variable; model dependent_variable = variable1 categorical_variable / archtest; output out=r r=yresid; run;
Note : Check P-value of Q statistics and LM tests. P-value greater than .05 indicates homoscedasticity.
Linearity: The relationship between the dependent variable and each independent variable should be approximately linear.
- Check: Plot the residuals against each predictor variable; residuals should show a random scatter pattern around zero.
- Fix: Consider transforming variables or using polynomial terms to achieve linearity.
Multicollinearity: Predictor variables should not be highly correlated with each other.
- Check: Calculate the variance inflation factor (VIF) for each predictor; VIF values above 5 or 10 indicate potential multicollinearity.
- Fix: If multicollinearity is detected, consider removing or combining correlated predictors.
Outliers: Identify extreme data points that may exert a significant influence on the model.
- Check: Plot the standardized residuals against the predicted values; look for points that deviate substantially from the others.
- Fix: If outliers are influential, consider excluding them or applying robust regression methods.
To learn more about the assumptions of multiple linear regression and how to treat them in SAS, check out the link below.
Detailed Assumptions of Multiple Linear Regression with SAS
Deepanshu founded ListenData with a simple objective - Make analytics easy to understand and follow. He has over 10 years of experience in data science. During his tenure, he worked with global clients in various domains like Banking, Insurance, Private Equity, Telecom and HR.
Share Share Tweet